فرمول اتحادها
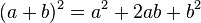

مربع سه جملهای
مکعب مجموع دو جمله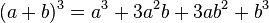
مزدوج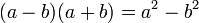
اتحاد جمله مشترک
مجموع و تفاضل مکعبات دوجمله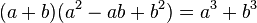

اویلر(اولر)
اتحاد لاگرانژ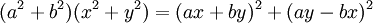
نیوتونی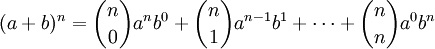
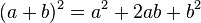

مربع سه جملهای
مکعب مجموع دو جمله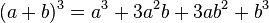
مزدوج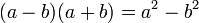
اتحاد جمله مشترک
مجموع و تفاضل مکعبات دوجمله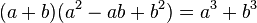

اویلر(اولر)
اتحاد لاگرانژ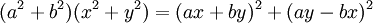
نیوتونی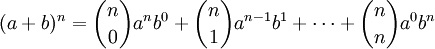
 اولین زن ریاضی دان که در تاریخ ریاضی از او نام برده شده : هیپاتیا
اولین زن ریاضی دان که در تاریخ ریاضی از او نام برده شده : هیپاتیا
اولین فرد شناخته شده ای که کشفیات ریاضی به او نسبت داده شده : تالس
اولین فردی که یک کتاب منسجم در هندسه منتشر کرد : بقراط خیوسی
اولین کسی که مقاطع مخروطی را ارائه کرد : منایخموس
اولین کسی که تلاش جدی در فلسفه ی ریاضی به عمل آورد : افلاطون
اولین ارائه دهنده ی نظریه ی اتمی بودن جهان : دموکریتوس
اولین کسی که در مسئله ی تضعیف مکعب به پیشرفت دست یافت : بقراط خیوسی
اولین ارائه دهنده ی برهان برای حل مسئله ی تثلیث زاویه به کمک مقاطع مخروطی : پاپوس
اولین فرد یونانی که ارتباطش با مسئله ی تربیع معلوم است : آناکساگوراس
اولین چاپ اصول اقلیدس : سال 1482
اولین فردی که ترجمه ی انگلیسی کاملی از اصول اقلیدس ارائه داد : بیلینگزلی
اولین کسی که کوشش کرد اصول ریاضی را تدوین کند : بقراط
اولین کسی که معادلات درجه دوم را به روش هندسی حل کرد : دیوفانتوس
اولین کسی که ترجمه ی عربی واقعا رضایت بخش از اصول اقلیدس ارائه کرد : ثابت ابن قره
اولین کسی که کتابی در حساب به زبان عربی تالیف کرد : خوارزمی
اولین نویسنده ی عربی نویس که با قضیه ی دو جمله ای در شکل مثلث پاسکال کار کرد : کاشانی
اولین نمونه ی کار ریاضی اصیل که توسط اعراب انجام شده : قائده ی ثابت ابن قره برای یافتن اعداد متحابه
اولین شرح منسجم از مثلثات مسطحه و کروی در اروپا که مستقل از نجوم مورد مطاعه قرار می گرفت :
تریانگولیس اومنیودیس اثر یوهان مولر
اولین کسی که علامت های + و – را به کار برد : یوهان ویدمان
 آیا میدانید google به چه معنی است؟
آیا میدانید google به چه معنی است؟Google از کلمه Googol گرفته شده است.
Googol هم اسم مستعار یک عدد است که توسط «میلتون سیروتا»
نامگذاری شده است.
عدد مذکور «ده به توان صد» است(به بزرگی این عدد دقت کنید)
انتخاب گوگل جنبه شعاری دارد.به این مفهوم که گوگل قصد دارد
تا سرویسها و خدمات و اهداف خود را به تمام جهان گسترش دهد.
به عدد «ده به توان ده به توان صد» گوگل پلکس(Googolplex) میگویند.
و به عدد «ده به توان ده به توان ده به توان صد»گوگل دوپلکس
(Googolduplex) میگویند.
1- در ایران به رشته های علوم پایه اهمیت نمی دهند ولی در کشورهای پیشرفته وضعیت کاملا متفاوت است و رشته هایی مثل ریاضی دارای ارزش زیادی هستند. این باور غلط اکثر دانشجویان رشته ی ریاضی در ایران است. واقعیت کاملا متفاوت است!!! از آنجایی که در کشورهای پیشرفته نظام سرمایه داری حاکم است رشته هایی که پولساز نباشند ارزش زیادی ندارند. رشته های علوم پایه مانند ریاضی، فیزیک و شیمی نیز جزو رشته هایی هستند که بطور مستقیم قابلیت پولسازی ندارند و در نتیجه بازار کاری مناسبی هم ندارند.
2- گزینه هایی که یک فارغ التحصیل ریاضی در خارج از ایران پیش روی خود می بیند تفاوت زیادی با داخل ایران ندارد. گزینه ی اول تدریس در مدرسه است که اولین پیش نیازش داشتن مدرک لیسانس Education هست (مدرک علوم پایه برای تدریس در مدارس مورد قبول نیست). علاوه بر اون باید دوره های مختلف آشنایی با تدریس و ادبیات انگلیسی رو گذروند که نیازمند صرف انرژی، زمان و هزینه ی زیادیست. البته جای تعجب نیست که فارغ التحصیلان کارشناسی ارشد یا دکتری ریاضی هرگز به تدریس در مدرسه فکر نکنند پس این گزینه عملا کنار می رود!!!
3- گزینه ی بعدی تدریس و تحقیق در دانشگاه است. با توجه به تعداد بسیار زیاد فارغ التحصیلان ریاضی که از سراسر دنیا جذب کشورهای پیشرفته می شود رقابت برای تصاحب کرسی استادی در دانشگاه ها به شدت زیاد است. اکثر کسانی که جذب دانشگاه ها می شوند دارای چند مدرک فوق دکترا (پست داک) از دانشگاه های معتبر همان کشورها هستند و دارای رزومه ی بسیار خوبی هستند (تعداد زیادی مقاله در ژورنال های معتبر منتشر کرده اند، تعداد زیادی سمینار در دانشگاه های مختلف ارائه کرده اند و سابقه ی سالها تدریس را در دوران ارشد، دکترا و فوق دکترا داشته اند). شانس اینکه به محض گرفتن مدرک دکترا به عنوان استاد جذب دانشگاه ها شوید بسیار اندک است مگر اینکه از دانشگاه های بسیار معتبر دنیا مثل هاروارد، پریسنتون، آکسفورد یا تورنتو مدرک دکترای خود را دریافت کرده باشید و رزومه ی بسیار خوبی هم داشته باشید. اگر به فکر برگشتن به ایران هستید در حال حاضر شانس استخدام به عنوان هیات علمی در دانشگاه های ایران هنوز وجود دارد اما با توجه به حجم عظیم فارغ التحصیلان دکترای داخل در سالهای پیش رو، پیش بینی وضعیت استخدام دانشگاه های در آینده مشخص نیست.
4- اگر به موقعیت های شغلی دیگر مثل محقق در شرکت های صنعتی فکر می کنید متاسفانه باید بدانید که اولا تعداد این موقعیت های شغلی بسیار محدود هستند و ثانیا این شرکت ها ترجیح می دهند محققانی را جذب کنند که صرفا دید تئوری و محض نداشته باشند و قابلیت های متناسب دیگری نیز داشته باشند مثلا به برنامه نویسی کامپیوتری یا نرم افزارهای آماری هم مسلط باشند.
5- تا اینجای متن بسیار ناامید کننده بود اما واقعیت همین است که گفته شد. حال راه چاره چیست؟ توصیه ی من به تمام دوستانی که در ایران مشغول تحصیل در مقطع لیسانس یا فوق لیسانس ریاضی هستند اینست که با توجه به پیش زمینه و علاقه شخصیشان به یکی از دو گرایش آمار یا کامپیوتر تغییر مسیر دهند. این دو رشته دارای بازار کاری بسیار خوبی در کشورهای پیشرفته هستند و کسانی که دید ریاضی دارند به سرعت می توانند خودشان را با این دو رشته تطبیق دهند. اگر امکان تغییر رشته در ایران یا گرفتن پذیرش در رشته های آمار یا کامپیوتر در خارج از ایران برایتان وجود ندارد سعی کنید گرایشهایی را انتخاب کنید که به آمار یا کامپیوتر نزدیک ترند یا موضوع پایان نامه ی خود را نزدیک به این دو رشته انتخاب کنید یا بطور شخصی به فراگیری برنامه نویسی کامپیوتری یا نرم افزارهای آماری بپردازید.
6- برای رشته ی کامپیوتر اول از همه باید دانش کلی کامپیوتریتون رو بالا ببرید. حتما دروس اصلی این رشته مثل ساختمان داده (Data Structure)، پایگاه داده (Database)، طراحی الگوریتم (Algorithm Design)، برنامه نویسی شی گرا (Object Oriented Programming) و یادگیری ماشینی (Machine Learning) رو مطالعه کنید. با مفاهیم پایه ای کامپیوتر مثل واحد پردازش مرکزی (CPU)، حافظه ی تصادفی (RAM)، سیستم عامل (Operating System)، کامپایلر و مفسر (Compiler and Interpreter)، حافظه ی هیپ و پشته (Heap and Stack) و پردازه و ریسه ی اجرایی (Process and Thread) آشنا باشید. روند تولید نرم افزار شامل تحلیل نیازمندی ها (Requirement Analysis)، طراحی نرم افزار (Design)، نوشتن کد (Writing)، تست کد (Testing)، اشکال زدایی کد (Debugging)، نوشتن راهنمای استفاده از نرم افزار (Documentation)، انتشار نرم افزار (Releasing) و نهایتا نگهداری و پشتیبانی نرم افزار (Maintenance and Support) رو بدونید. مفاهیم مهم ساختمان داده از جمله آرایه (Array)، لیست پیوندی (Linked List)، جدول هش (Hash Table) و درخت جستجوی دودویی (Binary Search Tree) و روند پیمایش، جستجو، حذف و اضافه (Traverse, Search, Add, and Delete) در اونها رو مطالعه کنید. همچنین با الگوریتم های مهم جستجو و مرتب سازی (Search and Sort) و پیچیدگی این الگوریتم ها (Algorithm Complexity) و مفاهیم مهم کدنویسی مثل اشاره گر (Pointer)، شی (Object)، کلاس (Class) و قالب (Template) آشنا باشید.
7- علاوه بر دانش کامپیوتری تا می تونید تجربه ی کدنویسی خودتون رو بیشتر و بیشتر کنید. در واقع دانش کامپیوتری صرفا بخش تئوری ماجراست و ارزش اصلی مربوط به قسمت کاربردی موضوع یعنی کد نویسی است. بهترین و جامع ترین زبان ها برای یادگیری ++C و Java هستند. سعی کنید تا می تونید کد بنویسید و پروژه های بزرگتر و پیچیده تر انجام بدید. مفاهیم کامپیوتری شاید خیلی سخت به نظر نرسند ولی کدنویسی نیاز به تمرین زیادی داره. بجای ویندوز سعی کنین با لینوکس کار کنید و دستورهای ترمینال لینوکس (Shell Scripting) رو یاد بگیرید. با نرم افزارهای مدیریت پایگاه داده مثل SQL، مدیریت فایل ها مثل Git و SVN و همچنین نرم افزارهای وب مثل JavaScript ،CSS ،HTML و PHP آشنا باشید.
8- برای رشته ی آمار هم ابتدا باید دانش کلی آماریتون رو بالا ببرید. حتما دروس اصلی این رشته مثل روش های آماری (Statistical Methods)، آمار ریاضی (Mathematical Statistics)، استنباط آماری (Statistical Inference)، نظریه ی احتمالات (Probability Theory)، فرایند تصادفی (Stochastic Process) و سری های زمانی (Time Series) رو مطالعه کنید. مفاهیم اولیه ی آماری رو یاد بگیرید مثل جمعیت (Population)، نمونه (Sample)، متغیر تصادفی (Random Variable)، میانگین (Mean)، میانه (Median)، انحراف معیار (Standared Deviation)، واریانس (Variance)، کوواریانس (Covariance) و همبستگی (Correlation) و همینطور انواع نمودار ها مثل نمودار نقطه ای (Scatter Plot)، نمودار جعبه ای (Box Plot) و هیستوگرام (Histogram). سعی کنید انواع گوناگون توزیع های گسسته و پیوسته رو مطالعه کنید مثل توزیع دو جمله ای (Binomial)، توزیع پواسون (Poisson)، توزیع نرمال (Normal)، توزیع گاوس (Gauss) و توزیع گاما (Gamma). با مفاهیم بنیادی آماری مثل تخمین (Estimation)، آزمون فرض (Hypothesis Testing)، بازه ی اطمینان (Confidence Interval) و مقدار پی (p-value) آشنا باشید.
9- مهمترین و اصلی ترین کاری که یک آماردان تجزیه و تحلیل داده هاست. برای این کار از روش هایی مثل رگرسیون (Regression)، آنالیز واریانس (Analysis of Variance)، روش های پارامتری و ناپارامتری (Parametric and Non-parametric) استفاده میشه. برای انجام این روش ها به نرم افزارهای آماری نیاز هست. از نرم افزارهای مقدماتی میشه به MS Excel و SPSS اشاره کرد که نیازی به کدنویسی زیاد ندارند. نرم افزارهای پیشرفته شامل R و SAS میشه که برای شما امکان کدنویسی و کار کردن با داده های بزرگ فراهم می کنند.
10- نکته ی آخر اینکه یکی از بهترین منابع موجود برای یادگیری کامپیوتر و آمار اینترنت هست که حجم عظیمی از اطلاعات رو بصورت رایگان در اختیار شما قرار میده. البته سایت های فارسی مفید شاید زیاد نباشند اما با تقویت زبان عمومی و تخصصی می تونید سایت های انگلیسی زیادی پیدا کنید و بدون نیاز به کلاس یا کتاب خودتون اقدام به یادگیری کنید.
1- فرض کنید روی یک کاغذ دو خط کشیده ایم که در یک نقطه با هم تقاطع دارند و می خواهیم محل تقاطع این دو خط را پیدا کنیم. برای این کار باید معادلات هر دو خط را بنویسیم (دو معادله ی خطی) و هدف پیدا کردن محل تقاطع روی صفحه است (دو مجهول). در نتیجه یک دستگاه معادلات خطی متشکل از دو معادله و دو مجهول داریم. اگر مجهولات را به شکل بردار مجهول، سمت راست معادلات را به شکل بردار معلوم و ضرایب مجهولات را به شکل ماتریس ضرایب نمایش دهیم، می توانیم دستگاه معادلات خطی را بصورت یک دستگاه ماتریسی نمایش دهیم و با حل آن محل تقاطع دو خط را بیابیم.
2- در ریاضیات، شاخه ی جبر خطی به بررسی و مطالعه ی بردارها، ماتریس ها، فضاهای برداری (فضاهای متشکل از بردارها همراه با دو عملگر جمع برداری و ضرب اسکالر)، تبدیلات خطی (توابع بین فضاهای برداری که ساختار فضای برداری را حفظ می کنند یعنی عمل جمع برداری و ضرب اسکالر را حفظ می کنند) و دستگاه های معادلات خطی (یا همان دستگاه های ماتریسی) و روش های حل آن می پردازد. کاربردی ترین قسمت جبر خطی همین بخش آخر یعنی روش های حل دستگاه های معادلات ماتریسی است چرا که بسیاری از مسائل علمی نهایتا به فرم یک دستگاه معادلات ماتریسی ساده می شوند و لذا حل آن ها از اهمیت خاصی برخوردار است.
3- برای حل دستگاه های ماتریسی روش های گوناگونی وجود دارد. اگر دستگاه ماتریسی را به فرم اولیه اش یعنی دستگاه خطی در نظر بگیریم می توانیم از روش هایی مثل روش حذف مجهولات و روش کرامر استفاده کنیم. مزیت این روش ها ساده بودن آنهاست اما اگر تعداد معادلات و مجهولات زیاد باشد این روش ها کارآمد نیستند. تبدیل دستگاه خطی به دستگاه ماتریسی باعث می شود که بتوانیم بسادگی با پیدا کردن وارون ماتریس ضرایب و ضرب آن در بردار سمت راست، جواب دستگاه را بیابیم. اما مشکل اینجاست که اگر اندازه ی ماتریس بزرگ باشد، پیدا کردن وارون آن براحتی امکان پذیر نیست. عموما در مسائل علمی واقعی اندازه ماتریس (یا همان تعداد معادلات و مجهولات بزرگ است) و همانطور که می بینید روش های ذکر شده اگر چه از نظر تئوری داری ارزش زیادی هستند اما در عمل کارآمد نمی باشند. اینجاست که نقش روش های جبرخطی عددی پررنگ می شود.
4- روش های جبرخطی عددی به دو دسته ی روش های مستقیم و غیر مستقیم تقسیم می شوند. از روش های مستقیم می توان به روش حذفی گاوس (تبدیل ماتریس ضرایب به ماتریس بالامثلثی یا پایین مثلثی)، روش تجزیه ی LU (تبدیل ماتریس ضرایب به ضرب یک ماتریس بالامثلثی و یک ماتریس پایین مثلثی)، روش تجزیه ی Cholesky (تبدیل ماتریس ضرایب به ضرب یک ماتریس پایین مثلثی و ترانهاده اش) و روش تجزیه ی QR (تبدیل ماتریس به ضرب یک ماتریس متعامد و یک ماتریس بالا مثلثی) اشاره نمود.
5- اگرچه برای ماتریس های بزرگ، روش های عددی مستقیم، کارآمدتر از روش های غیرعددی هستند اما اگر اندازه ی ماتریس بسیار بزرگ باشد، روش های عددی مستقیم نیز کارآمدی خود را از دست می دهند و باید از روش های عددی غیرمستقیم (یا تکراری) استفاده کرد. از بین این روش ها می توان به روش ژاکوبی (تبدیل ماتریس ضرایب به جمع یک ماتریس قطری و یک ماتریس با قطر صفر)، روش گاوس - سایدل (تبدیل ماتریس ضرایب به جمع یک ماتریس بالامثلثی و یک ماتریس پایین مثلثی)، روش SOR (تبدیل ماتریس ضرایب به جمع یک ماتریس قطری، یک ماتریس بالامثلثی و یک ماتریس پایین مثلثی) و روش های زیر فضای Krylov اشاره نمود.
 ,تست تمرکز جالب،عدد ۱۰۰۰ رو فرض کنید. ۴۰ رو به اون اضافه کنید. حاصل رو با ۱۰۰۰ دیگر جمع کنید. عدد ۳۰ رو به جواب اضافه کنید. با ۱۰۰۰ دیگر جمع کنید. حالا ۲۰ تا دیگر به حاصل جمع،اضافه کنید.با ۱۰۰۰ تای دیگر جمع کنید و نهایتاً ۱۰ تا دیگر به حاصل اضافه کنید.
,تست تمرکز جالب،عدد ۱۰۰۰ رو فرض کنید. ۴۰ رو به اون اضافه کنید. حاصل رو با ۱۰۰۰ دیگر جمع کنید. عدد ۳۰ رو به جواب اضافه کنید. با ۱۰۰۰ دیگر جمع کنید. حالا ۲۰ تا دیگر به حاصل جمع،اضافه کنید.با ۱۰۰۰ تای دیگر جمع کنید و نهایتاً ۱۰ تا دیگر به حاصل اضافه کنید. این جمع را با باید با ذهنتان انجام دهید، نه با ماشین حساب.برای جواب برید ادامه مطلب
لطفا خودتان را معرفی کرده و بفرمایید از چه سالی دانش آموز کانون بوده اید؟
پژمان شهبازی هستم از دبیرستان شهيداژه اى اصفهان .سال چهارم دبیرستان را در آزمون های کانون شرکت کردم
به چه علت تصمیم گرفتید در آزمون های کانون شرکت کنید؟
به دلیل اینکه فواصل زمانی برگزاری آزمون های کانون خوب ومناسب بود و فاصله ی زمانی بین دو آزمون نه زیاد بود نه کم و دلیل دیگر اینکه برادرم هم در سال های گذشته در آزمون های کانون شرکت داشتند و رتبه ایشان در کنکور سال هشتاد ونه 26 شد و آزمون های کانون از جامعه ی آماری بالایی برخوردار است.
فکر می کنید شرکت در آزمون های کانون چقدر در موفقیت شما تاثیر گذار بوده است؟
خوب مسلما شرکت در آزمون های کانون تاثیر گذار بود و من توانستم با استفاده از برنامه راهبردی بهتر و منسجم تر درس بخوانم و برنامه ی دو هفته یکبار آزمون دادن را در دستور کار خود داشته باشم و خودم را محک بزنم و طبق برنامه درس خواندن بسیار مفید است
لطفا از نحوه برنامه ریزی و ساعات مطالعاتی خود بگویید؟
با توجه به روزهای هفته برنامه داشتم و اینکه چقدر زمان برای مطالعه دارم.به طبع روزهای تعطیل ساعات مطالعاتی بیشتری داشتم به طور میانگین 8 ساعت مطالعه و در روزهایی که مدرسه می رفتم کمتر بود.بیشتر زمانم را به دروس اختصاصی ،اختصاص دادم و تا قبل عید بیشتر بر دروس اختصاصی تسلط پیدا کردم ولی این به این معنی نیست که دروس عمومی را کنار بگذارم و دروس عمومی را هم می خواندم ولی کمتر و بعد عید روی دروس عمومی تمرکز بیشتری کردم.
آیا در درسی ضعف داشتید که آن را به نقطه قوت مبدل نمایید ؟
باید بگویم در همه ی دروس به طور متعادل تسلط داشتم و درس خاصی به نظرم نمی آید که مشکل زیادی در آن داشته باشم فقط در درس شیمی بی دقتی زیادی در سر جلسه آزمون ها می کردم .مثلا بی دقتی هایم اینگونه بود که سوال را کامل و درست نمی خواندم و به خواسته مساله دقت نمی کردم و برای انتخاب گزینه به اشتباه می افتادم که این نقطه ضعف را سعی کردم برطرف کنم و سوالات را کامل و به دقت بخوانم و بدانم خواسته مساله چیست و درست جایگذاری کنم.
آیا از کتاب های آموزشی کانون استفاده می کردید؟
بله –از کتاب های آبی قلمچی برای چنددرس اختصاصی استفاده کردم ،برای دروس ریاضیات،هندسه تحلیلی، ریاضیات گسسته از کتاب های کانون برای تست زنی استفاده کردم که خوب و مفید بود.
آیا شما یک برنامه برای آزمون ها داشتید؟
بله –بنده برنامه راهبردی کانون را دنبال می کردم که با کمک آن توانستم خوب پیش بروم .
نظرتان را راجع به آزمون های کانون در طی سال و همین طور آزمون های جامع بفرمایید؟
دروس اختصاصی آزمون ها همیشه خوب بودند البته گاهی پیش می آمد که سوالات سخت تر باشد ولی درکل از سطح علمی سوالات راضی بودم .سوالات دروس عمومی سخت تر از کنکور بود و در کنکور 94 به نظرم سوالات آسان تر بود.
آیا شما پشتیبان ویژه داشتید ؟
بله –آقای امید چهره گشا رتبه 5 کشوری سال 93 پشتیبان ویژه من بودند که از ایشان راضی بودم . با ایشان در طول سال و همین طور دوران جمع بندی گفتگو می کردم و راهنمایی های ایشان برایم مفید و مثمر ثمر بود.
او در مقدمه ی كتابش می نویسد : « پدرم اهل پیزا بود و در اداره ی گمرك بوكیا درافریقا كار می كرد . او مرا با خود به آنجا برد تا هنر حساب كردن را یاد بگیرم . هنر عجیب حساب كردن ، تنها به كمك نه علامت هندی ، مرا چنان به شوق آورد كه ، به طور قطع ، تصمیم گرفتم ، آن چه را در مصر ، یونان ، سوریه ، سیسیل و پرووانس در این باره می دانستند ، بیاموزم . از همه ی این كشور ها دیدن كردم و قانع شدم كه ، دستگاه عدد نویسی هندی از همه كامل تر است و بر روش فیثاغورث برتری دارد . این دستگاه را ، و همه ی آنچه به آن مربوط می شد ، یاد گرفتم ، و بررسی های شخصی خودم را كه از « مقدمات » اقلیدس به دست آورده بودم ، به آن اضافه كردم و تصمیم گرفتم این كتاب را بنویسم » .
« كتاب حساب » رساله ای است درباره ی حساب و جبر كه شامل 15 فصل است و آگاهی هایی از دانش حساب و جبر آن زمان را ، در اختیار خواننده می گذارد .
لئوناردوی پیزایی ، با طرح و حل مساله ای درباره ی سرمایه ی چند نفر ، برای نخستین بار ، اندیشه ی عدد منفی را ، به نام «قرض » ، در اروپا طرح كرد .
خدمت بزرگ لئوناردوی پیزایی به دانش ، در این بود كه ، برای نخستین بار ، دانشمندان اروپایی را با جبر و دستگاه عدد نویسی هندی آشنا كرد .
كار علمي لايب نيتس ، با فعاليت دولتي او به عنوان فرستاده ي سياسي به پاريس مخلوط شده بود . در سال 1673 در انگلستان بود و در آنجا ، ماشين حسابي را كه خود او – بعد از آشنايي با ماشين حساب پاسكال – ساخته بود ، در جامعه ي سلطنتي به نمايش گذاشت . بعد از آنكه به پاريس بازگشت ، به عضويت جامعه ي سلطنتي انتخاب شد .
لايب نيتس ، هم زمان با نيوتون و بدون رابطه با او ، به آناليز رياضي معاصر – حساب ديفرانسيل و انتگرال – دست يافت .
او مقدمات نظريه ي دترمينان ها را ، كه ضمن حل دستگاه هاي درجه اول چند مجهولي پديد آمده بود ، طرح ريخت . لايب نيتس ، به جز اينها ، كار هاي زيادي درباره ي ويژگي هاي منحني ها و تجزيه ي تابع ها به رشته دارد كه منجر به نتيجه گيري هاي مهمي شد .
ايزاك نيوتون (1727 – 1642) رياضيدان و فيزيك دان انگليسي
نيوتون كشاورز زاده بود و پدرش قبل از تولد پسر خود از دنيا رفت . دانشمند آينده ، از همان دوران كودكي ، گرايش خود را به كار مستقل و آموزش جدي نشان داد . در دانشگاه كمبريج تحصيل كرد و در آنجا بود كه معلمان را از استعداد رياضي خود ، دچار حيرت كرد . بعد ها استاد همين دانشگاه شد . از سال 1703 ، رئيس جامعه ي سلطنتي (فرهنگستان علوم) لندن شد كه بسياري از دانشمندان طراز اول آن زمان را ، در خود جمع كرده بود .
ايزاك نيوتون ، مؤلف كتاب مشهور « مباني رياضي فلسفه ي طبيعي » است (1687) ، كه در آن ، قانون هاي مشهور نيوتون در زمينه ي مكانيك و يك رشته كشف هاي ديگر را ، مطرح كرده است . در سال 1787 ، كتاب « حساب عمومي » را نوشت كه در آن ، از روش جبري با نشانه ها و طرح ريزي امروزي ، صحبت كرده است .
او براي نخستين بار ، پرتو هاي نوراني را مورد مطالعه قرار داد و از آنجا ويژگي رنگ ها را كشف كرد ، چيزي كه تا آن زمان ، هيچكس درباره ي آن حدس هم نزده بود .
نيوتون و لايبنيتس را به عنوان پايه گذاران علم حساب ديفرانسيل و انتگرال مي شناسند . نيوتون در اواسط دهه ي 1660 به اين افكار دسترسي يافت ، در حالي كه لايبنيتس كار خود را از اوايل دهه ي 1670 آغاز كرد . اما لايبنيتس آنها را زودتر به چاپ رساند و علامت گذاري هاي او بسيار جالبتر از علامت گذاري هاي نيوتون بود .
بسياري از روش ها و مطالب اين علم قبلا هم كشف شده بودند ، حتي بارو معلم نيوتون در كمبريج ، بدون اطلاع از مفهوم دقيق مشتق و انتگرال ، يك معادل هندسي قضيه ي بنيادي را بيان و اثبات كرده بود . در حقيقت نيوتون و لايبنيتس پلي استوار بين ايده هاي قبلي و روش هاي مدرن در رابطه با اين دانش را بنا نهاده اند .
روش مختصاتي ، به دكارت و فرما امكان داد تا هندسه ي تحليلي را به وجود آورند . در هندسه ي تحليلي ، مي توان هندسه را از نظر معادله هاي جبري مورد بررسي قرار داد. دكارت ، نظريه ي معادله ها را با وارد كردن نشانه هاي تازه اي ، غني تر و ساده تر كرد . او نخستين كسي بود كه نشانه هاي x و y و z را براي مجهول انتخاب كرد (او براي z ارجحيت قائل بود ) . همچنين ، روش ضريب هاي نامعين را كشف كرد كه امروزه كاربرد هاي فرواني دارد . دكارت ، در فلسفه و رياضيات ، از روش تحليلي پيروي مي كرد كه طبق آن ، بايد هر مساله را به اجزاء تشكيل دهنده اش تجزيه كرد و سپس با آغاز از ساده ترين جزء ها ، به طرف مورد هاي بغرنج تر حركت كرد .